Zipformer 模型详解

摘要¶

Zipformer 是新一代 kaldi 团队最新研发的序列建模模型。相比较于 Conformer、Squeezeformer、E-Branchformer 等主流 ASR 模型，Zipformer 具有 效果更好、计算更快、更省内存 等优点。Zipformer 在 LibriSpeech、Aishell-1 和 WenetSpeech 等常用数据集上取得了 当前最好 的 ASR 结果。

本期文章将解析 Zipformer 的具体创新点，主要包括： - 高效的模型结构：Downsampled encoder structure 和 Zipformer block - 新 normalization：BiasNorm - 新激活函数：Swoosh - 新优化器：ScaledAdam 优化器 - 激活值限制：Balancer 和 Whitener

建议读者阅读论文了解更多细节：https://arxiv.org/pdf/2310.11230.pdf

方法¶

1. Downsampled encoder structure¶

图 1 展示了 Zipformer 总体框架图，由一个 Conv-Embed 模块和多个 encoder stack 组成。不同于 Conformer 只在一个固定的帧率 25Hz 操作，Zipformer 采用了一个类似于 U-Net 的结构，在不同帧率上学习不同时间分辨率的时域表征。

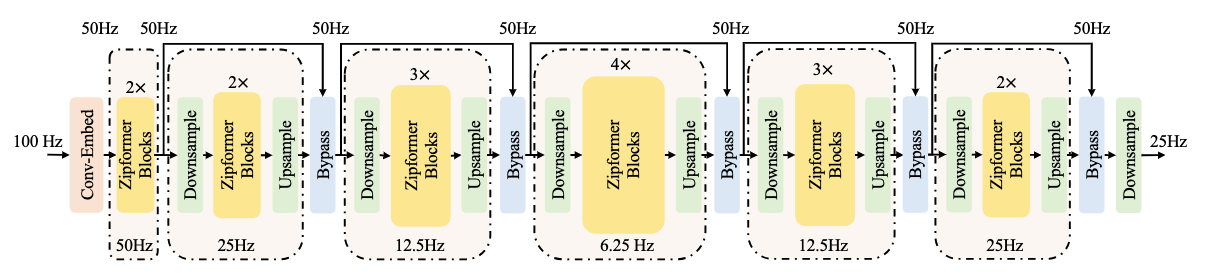
图1：Zipformer 总体框架

首先，Conv-Embed 将输入的 100Hz 的声学特征下采样为 50 Hz 的特征序列；然后，由 6 个连续的 encoder stack 分别在 50Hz、25Hz、12.5Hz、6.25Hz、12.5Hz 和 25Hz 的采样率下进行时域建模。除了第一个 stack 外，其他的 stack 都采用了降采样的结构。在 stack 与 stack 之间，特征序列的采样率保持在 50Hz。不同的 stack 的 embedding 维度不同，中间stack 的 embedding 维度更大。每个 stack 的输出通过截断或者补零的操作，来对齐下一个 stack 的维度。Zipformer 最终输出的维度，取决于 embedding 维度最大的 stack。

对于降采样的 encoder stack，成对出现的 Downsample 和 Upsample 模块负责将特征长度对称地放缩。我们采用几乎最简单的方法实现 Downsample 和 Upsample 模块。例如，当降采样率为 2 时，Downsample 学习两个标量权重，用来将相邻的两帧加权求和了；Upsample 则只是简单地将每一帧复制为两帧。最后，通过一个 Bypass 模块，以一种可学习的方式结合 stack 的输入和输出。

2. Zipformer block¶

Conformer block 由四个模块组成：feed-forward、Multi-Head Self-Attention (MHSA)、convolution、feed-forward。MHSA 模块通过两个步骤学习全局时域信息：基于内积计算注意力权重，以及利用算好的注意力权重汇聚不同帧的信息。 然而，MHSA 模块通常占据了大量的计算，因为以上两步操作的计算复杂度都是平方级别于序列长度的。因此，我们将 MHSA 模块根据这两个步骤分解为两个独立的模块：Multi-Head Attention Weight (MHAW) 和 Self-Attention (SA)。 这样一来，我们可以 通过在一个 block 里面使用一个 MHAW 模块和两个 SA 模块，以高效的方式实现两次注意力建模。此外，我们还提出了一个 新的模块 Non-Linear Attention (NLA) ，充分利用已经算好的注意力权重，进行全局时域信息学习。

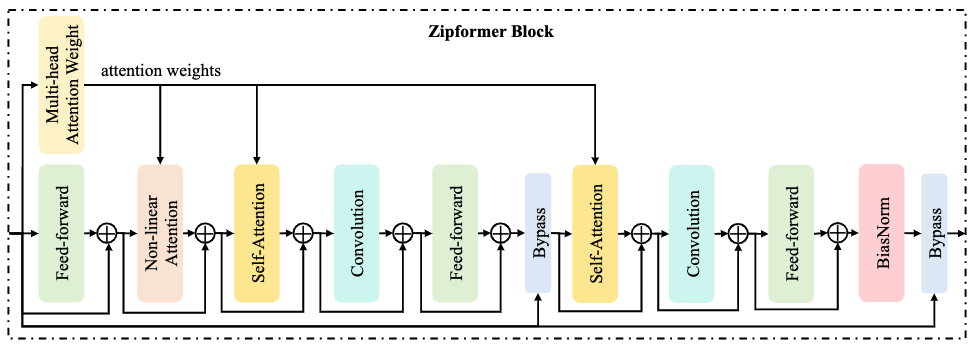
图2：Zipformer block 结构图

图 2 展示了 Zipformer block 的结构图，其深度大约是 Conformer block 的两倍。核心的思想是通过复用注意力权重来节省计算和内存。 具体而言，block 输入先被送到 MHAW 模块计算注意力权重，并分享给 NLA 模块和两个 SA 模块使用。同时，block 输入也被送到 feed-forward 模块，后面接着 NLA 模块。接着是两个连续的模块组，每组包含 SA、convolution 和 feed-forward。最后，由一个 BiasNorm 模块来将 block 输出进行 normalize。除了普通的加法残差连接，每个 Zipformer block 还使用了两个 Bypass 模型，用于结合 block 输入和中间模块的输出，分别位于 block 的中间和尾部。值得注意的是，我们并没有像常规的 Transformer 模型一样，对每个模块都使用 normalization layer 去周期性地调整激活值的范围，这得益于我们使用的 ScaledAdam 优化器可以为各个模型自动学习参数的 scale。

Non-Linear Attention¶

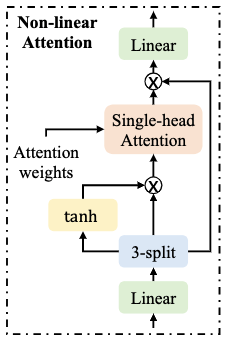
图 3 展示了 NLA 模块的结构。类似于 SA 模块，它利用 MHAW 模块计算好的注意力权重，沿着时间轴汇聚不同帧的向量。 具体而言，它使用三个 linear 将输入转换为 A、B、C，每个的维度为输入维度的 ¾ 倍。模块的输出为 $linear(A ⊙ attention(tanh(B) ⊙ C))$，⊙ 表示点乘，$attention$ 表示利用一个注意力头的权重对不同帧汇聚，$linear$ 负责恢复特征的维度。

图 3：Non-Linear Attention 模块

Bypass¶

Bypass 模块学习一个逐通道的权重 $\mathbf{c}$，结合模块输入 $\mathbf{x}$ 和模块输出 $\mathbf{y}$：$(1-\mathbf{c}) \odot \mathbf{x} + \mathbf{c} \odot \mathbf{y}$。我们发现，在训练早期通过约束 $\mathbf{c}$ 的最小值让模块接近 “straight-through” 有助于稳定模型训练。

3. BiasNorm¶

Conformer 使用 LayerNorm 来 normalize 激活值，给定 $D$ 维的向量 $\mathbf{x}$。LayerNorm 的公式为：

\[ \mathrm{LayerNorm}(\mathbf{x}) = \frac{\mathbf{x} - \mathrm{E}[\mathbf{x}]}{\sqrt{\mathrm{Var}[\mathbf{x}]+ \epsilon}} \odot \boldsymbol\gamma + \boldsymbol\beta. \]

LayerNorm 先计算均值 $\mathrm{E}[x]$ 和方差 $\mathrm{Var}[x]$，用于向量标准化，将向量长度调整调整为 $\sqrt{D}$ 。然后，利用逐通道的放缩因子 $\boldsymbol\gamma$ 和偏置 $\boldsymbol\beta$ 进行元素变换，这有助于调整不同模块对整个模型的相对贡献。

然而，我们观察到使用 LayerNorm 的 Conformer 模型存在着两种失败的情况：1）有时候会将某个特征维度设置得非常大，例如 50 左右，我们认为这是模型在抵制 LayerNorm 完全消除长度的机制，这个非常大的数可以在 normalize 的过程中保留其他维度的一部分长度信息。 2）有些模块（例如 feed-forward 和 convolution）的输出值非常小，例如 1e-6。我们认为在模型开始训练的时候，还没有学到有用信息的模块被防缩因子 $\boldsymbol\gamma$ 通过接近 0 关闭了。如果放缩因子 $\boldsymbol\gamma$ 在 0 左右震荡，反向传播的梯度也会随之翻转，这样一来，模块很难学到有用的信息，因为这是一个难以跳出的局部鞍点。

为了解决上述问题，我们提出 BiasNorm 模块来替换 LayerNorm：

\[ \mathrm{BiasNorm}(\mathbf{x}) = \frac{\mathbf{x}}{\mathrm{RMS}[\mathbf{x} - \mathbf{b}]} \cdot \exp(\gamma) \]

其中，$\mathbf{b}$ 是可学习的逐通道的 bias，$\gamma$ 是一个可学习的标量。首先，我们去除了减均值的操作，因为它没有必要，除非它接着一个非线性变换。 $\mathbf{b}$ 充当一个非常大的数，用于在 normalize 的过程中保留向量的一部分长度信息，这样一来，模型就不需要牺牲一个额外的维度来做这个事情。 这或许有助于模型量化，因为它可以减少离群点的出现。由于 $\exp(\gamma)$ 一直是正数，避免了出现梯度方向翻转导致的某些模块无法学习的问题。

4. Swoosh 激活函数¶

Conformer 采用的激活函数为 Swish，其公式为：

\[ \mathrm{Swish}(x) = x \cdot (1+\exp(-x))^{-1}. \]

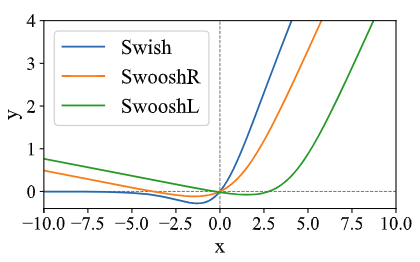
我们提出两个新的激活函数用于代替 Swish，分别称为 SwooshR 和 SwooshL：

\[ \begin{split} \mathrm{SwooshR}(x) &= \log(1 + \exp(x-1)) - 0.08x - 0.313261687, \\ \mathrm{SwooshL}(x) &= \log(1 + \exp(x-4)) - 0.08x - 0.035. \end{split} \]

在 SwooshR 函数中，偏移值 0.313261687 是为了让函数经过原点；在 SwooshL函数中，偏移量 0.035 是经过实验调过的，比让它精确经过原点的结果略好。

如图 4 所示，SwooshL 近似于 SwooshR 向右偏移得到的。“L” 和 “R” 表示两个与 x 轴的交点中哪个靠近或经过原点。类似于 Swish，SwooshR 和 SwooshL 都是有下确界的并且非单调的。 相比较于 Swish，最大的区别在于 SwooshR 和 Swoosh 对于负数部分有一个斜率，这个可以避免输入一直是负数以及避免 Adam-type 的更新量分母（二阶梯度动量）太小。当将 SwooshR 用在 Zipformer 各个模块中时，我们发现，那些带残差的模块， 例如 feed-forward 和 ConvNeXt，倾向于在激活函数前面的线性层中学习一个绝对值较大的负数 bias，以学习一种 “normally-off” 的行为。 因此，我们把 SwooshL 函数用在这些 “normally-off” 的模块中，把 SwooshR 用在其他的模块：convolution 和 Conv-Embed 剩下的部分。

图4：激活函数 Swish，SwooshR 和 SwooshL

5. ScaledAdam¶

我们提出一个 Adam 优化器的 parameter-scale-invariant 版本，称为 ScaledAdam，它可以加快模型收敛。一方面，ScaledAdam 根据参数 scale 放缩参数更新量，来确保不同 scale 的参数相对变化一致；另一方面，ScaledAdam 显式学习参数的 scale，这相当于给了一个额外的放缩参数 scale 的梯度。

令 $f(\boldsymbol\theta)$ 为我们想要优化的 loss 函数，它对参数 $\boldsymbol\theta$ 是可导的。在每个步骤 $t$，Adam 计算参数梯度 $\mathbf{g}_t = \nabla_{\boldsymbol\theta}f(\boldsymbol\theta_{t-1})$，并更新梯度的一阶动量 $\mathbf{m}_t = \beta_1 \cdot \mathbf{m}_{t-1} + (1-\beta_1) \cdot \mathbf{g}_t$ 和二阶动量 $\mathbf{v}_t = \beta_2 \cdot \mathbf{v}_{t-1} + (1-\beta_2) \cdot \mathbf{g}_t^2$，此处, $\beta_1, \beta_2 \in [0, 1) $ 表示控制动量更新的系数。Adam 在步骤 t 的参数更新量为：

\[ \boldsymbol\Delta_t = \alpha_t \cdot \frac{\sqrt{1-\beta_2^t}}{1-\beta_1^t} \cdot \frac{\mathbf{m}_t}{\sqrt{\mathbf{v}_t}+\epsilon}, \]

式中，$\alpha_t$ 通常由外部的 LR schedule 控制，$\frac{\sqrt{1-\beta_2^t}}{1-\beta_1^t}$ 为偏置纠正项。尽管 Adam 对梯度 scale 是 invariant 的，但是我们认为它仍然存在两个问题：1）更新量 $\boldsymbol\Delta_t$ 并没有考虑参数的 scale（标记为 $r_{t-1}$），对于参数的相对更新量 $\boldsymbol\Delta_t/r_{t-1}$ 而言，Adam 可能会导致对 scale 小的参数学习太快，或者对 scale 大的参数学习太慢。 2）我们很难直接学习参数的 scale，因为参数 scale 的大小变化方向是高维度的梯度向量中一个特别具体的方向。尤其是 scale 变小的方向更加难学，因为在优化的过程中，梯度会引入噪声，参数的 scale 会倾向于不断增大。

Scaling update¶

为了确保不同 scale 的参数的相对变化量 $\boldsymbol\Delta_t/r_{t-1}$ 一致，我们**在参数更新量中引入参数的 scale，来放缩更新量**：

\[ \boldsymbol\Delta_t' = \alpha_t \cdot r_{t-1} \cdot \frac{\sqrt{1-\beta_2^t}}{1-\beta_1^t} \cdot \frac{\mathbf{m}_t}{\sqrt{\mathbf{v}_t}+\epsilon}. \]

我们计算 $\mathrm{RMS}[\boldsymbol\theta_{t-1}]$ 作为参数的 scale $r_{t-1}$。由于 ScaledAdam 比 Adam 更不容易发散，我们使用一个不需要很长 warm-up 的 LR schedule，称为 Eden；我们使用明显更大的学习率，因为参数的 RMS 值通常小于 1。

Learning parameter scale¶

为了显式学习参数的 scale，我们在将它当作一个真的存在的参数一样学习，仿佛我们将每个参数分解为 $ \boldsymbol\theta = r \cdot \boldsymbol\theta'$，并且我们是对参数 scale $r$ 和内部参数 $\boldsymbol\theta'$ 进行梯度下降。值得注意的是，在具体实现中，我们并没有将每个参数进行分解，只是增加了一个额外的更新参数 scale 的梯度。

令 $h$ 为参数 scale 的梯度，存在 $h_t = \nabla_{r}f(\boldsymbol\theta_{t-1}) = \mathbf{g}_t \cdot \boldsymbol\theta_{t-1}'$。由于 Adam 对梯度的 scale 几乎是 invariant 的，我们可以计算 $h_t = \mathbf{g}_t \cdot (r_{t-1} \odot \boldsymbol\theta_{t-1}') = \mathbf{g}_t \cdot \boldsymbol\theta_{t-1}$。按照 Adam 算法，我们维护参数 scale 梯度 $h_t$ 的一阶动量 $n_t = \beta_1 \cdot n_{t-1} + (1-\beta_1) \cdot h_t$ 和二阶动量 $w_t = \beta_2 \cdot w_{t-1} + (1-\beta_2) \cdot h_t^2$。将参数 scale 从 $r_{t-1}$ 更新到 $r_{t}$ 对参数 $ \boldsymbol\theta$ 带来的变化为 $\boldsymbol\Delta_{t,r}' = (r_t - r_{t-1}) \odot \boldsymbol\theta_{t-1}'$。同样地，我们放缩参数 scale 对应的更新量：

\[ \begin{split} \boldsymbol\Delta_{t,r}' &= \eta \cdot \alpha_t \cdot r_{t-1} \cdot \frac{\sqrt{1-\beta_2^t}}{1-\beta_1^t} \cdot \frac{n_t}{\sqrt{w_t}+\epsilon} \odot \boldsymbol\theta_{t-1}' \\ &= \eta \cdot \alpha_t \cdot \frac{\sqrt{1-\beta_2^t}}{1-\beta_1^t} \cdot \frac{n_t}{\sqrt{w_t}+\epsilon} \odot \boldsymbol\theta_{t-1}. \end{split} \]

式中， $\eta$ 用于放缩学习率，我们发现设置为 0.1 有助于稳定训练。此时，参数的更新量由 $\boldsymbol\Delta_{t}'$ 变为 $\boldsymbol\Delta_{t,r}' + \boldsymbol\Delta_{t}'$，这等价于额外引入一个放缩参数 scale 的梯度。 这个改动有助于我们简化模型结构，我们可以去掉大部分的 normalization 层，因此每个模块可以更容易得学习参数 scale ，来将激活值调整到一个合适的范围。

Eden schedule¶

Eden schedule 的公式如下：

\[ \alpha_t = \alpha_{\mathrm{base}} \cdot \left(\frac{t^2 + \alpha_{\mathrm{step}}^2}{\alpha_{\mathrm{step}}^2}\right)^{-0.25} \cdot \left(\frac{e^2 + \alpha_{\mathrm{epoch}}^2}{\alpha_{\mathrm{epoch}}^2}\right)^{-0.25} \cdot \mathrm{linear}(\alpha_{\mathrm{start}}, t_{\mathrm{warmup}}, t). \]

式中，$t$ 为 step，$e$ 为 epoch，$\alpha_{\mathrm{step}}$ 和 $ \alpha_{\mathrm{epoch}}$ 分别控制学习率在哪个 step 和 epoch 开始快速下降，$\mathrm{linear}(\alpha_{\mathrm{start}}, \alpha_{\mathrm{warmup}}, t)$ 表示一个线性 warmup，起点为 $\alpha_{\mathrm{start}}$，经过 $\alpha_{\mathrm{warmup}}$ 个 step 变为 1。$\alpha_{\mathrm{base}}$ 表示当没有 warmup 的情况下学习率的最大值。让 Eden 同时依赖于 step 和 epoch 两个变量，是为了让模型的更新程度在经过一定的训练数据量（e.g., 1h）时，几乎不受 batch size 影响。 Eden 公式中，epoch 也可以替换为其他合适的变量，如经过多少小时的数据。

Efficient implementation¶

为了加快 ScaledAdam 计算，我们将参数根据 shape 分组，按照 batch 进行参数更新， 值得注意的是这并不影响结果。Scaleadam 需要的内存使用量和 Adam 差不多，只需要额外的内存来存储参数 scale 对应梯度的一阶动量和二阶动量 $n_t$ 和 $w_t$。

6. 激活值限制¶

为了确保训练的一致性以及避免训练出性能差的模型，我们提出 Balancer 和 Whitener，用于约束模型的激活值。 Balancer 和 Whitener 以一种省内存的方式实现：在前向过程中，相当于是一个 no-op；在反向过程中，计算一个对激活值施加限制的损失函数的梯度 $\mathbf{g}'$，加到原本的激活值梯度 $\mathbf{g}$ 上：$\mathbf{g} = \mathbf{g} + \mathbf{g}'$。 Balancer 和 Whitener 的应用位置没有遵循一个明确的规则，我们一般是在模型表现不好的时候，通过分析模型哪个地方出现问题，再对应地使用 Balancer 和 Whitener 去修复模型。

Balancer¶

在每个特征通道上的分布上，我们观察到 两种失败的模式： 1） 有时候值的范围太大或太小，这个可能导致训练不稳定，尤其是使用半精度训练的时候。 2） 如果我们看 feed-forward 模型中激活函数前面的线性层的神经元，很多的值是负数，这个造成了参数浪费。

Balancer 通过对激活值施加限制：最小和最大平均绝对值， 分别标记为 $a_{\mathrm{min}}$ 和 $a_{\mathrm{max}}$；最小和最大正数比例， 分别标记为 $p_{\mathrm{min}}$ 和 $p_{\mathrm{max}}$。由于正数比例是不可导的，我们将限制转化为 standard-deviation-normalized mean $\mathrm{E/\sqrt{Var}}$：$f_{\mathrm{pos}\rightarrow\mathrm{E/\sqrt{Var}}}(x) = \mathrm{arctanh}(2x - 1) / (\sqrt{\pi}\cdot\log2)$，得到 $\mu_{\mathrm{min}} = f_{\mathrm{pos}\rightarrow\mathrm{E/\sqrt{Var}}}(p_{\mathrm{min}})$ 和 $\mu_{\mathrm{max}} = f_{\mathrm{pos}\rightarrow\mathrm{E/\sqrt{Var}}}(p_{\mathrm{max}})$。同时，我们将平均绝对值转化为 RMS：$f_{\mathrm{abs}\rightarrow\mathrm{RMS}}(x) = \sqrt{\pi/2} \cdot x$，得到 $r_{\mathrm{min}} = f_{\mathrm{abs}\rightarrow\mathrm{RMS}}(a_{\mathrm{min}})$ 和 $r_{\mathrm{max}} = f_{\mathrm{abs}\rightarrow\mathrm{RMS}}(a_{\mathrm{max}})$。具体而言，对于激活值 $\mathbf{x}$，限制函数定义为：

\[ \begin{split} \mathcal{L}_{\mathrm{RMS}} &= |\log(\min(\max(\mathrm{RMS}[\mathbf{x}], r_{\mathrm{max}}),r_{\mathrm{min}})/\mathrm{RMS}[\mathbf{x}] )|, \\ \mathcal{L}_{\mathrm{E/\sqrt{Var}}} &= | \mathrm{E}[\mathbf{x}] / \sqrt{\mathrm{Var}[\mathbf{x}]} - \mathrm{clamp}(\mathrm{E}[\mathbf{x}] / \sqrt{\mathrm{Var}[\mathbf{x}]}, \mu_{\mathrm{min}}, \mu_{\mathrm{max}})|, \\ \mathcal{L}_{\mathrm{balancer}} &= \mathcal{L}_{\mathrm{RMS}} + \mathcal{L}_{\mathrm{E/\sqrt{Var}}}, \end{split} \]

式中，$\mathrm{RMS}[\mathbf{x}]$，$\mathrm{E}[\mathbf{x}]$ 和 $\sqrt{\mathrm{Var}[\mathbf{x}]}$ 为每个通道的统计量。

Whitener¶

激活值的 另一种失败的模式 是： 协方差矩阵的特征值中，有一个或者少数几个特征值占据主导，剩下的特征值都特别小。这个现象通常发生在即将训练奔溃的模型中。

Whitener 模块旨在通过限制协方差矩阵的特征值尽可能相同，来鼓励模块学习更有信息量的输出分布。 具体而言，对于特征 $\mathbf{x} \in \mathcal{R}^{N \times D}$，我们计算协方差矩阵 $C = (\mathbf{x} - \mathrm{E}[\mathbf{x}])^T(\mathbf{x} - \mathrm{E}[\mathbf{x}])$，$\mathrm{E}[\mathbf{x}]$ 为各个通道的均值。Whitener 定义的限制函数为：

\[ \begin{split} \mathcal{L}_{\mathrm{whitener}} &= (\sum_i \lambda_i^2/D) / (\sum_i \lambda_i/D)^2 \\ &= (\sum_{i}\sum_{j}C_{i,j}^2/D) / (\sum_{i}C_{i,i}/D)^2, \\ \end{split} \]

式中，$\boldsymbol\lambda=\{\lambda_1, \dots, \lambda_D\}$ 为协方差矩阵的特征值。

实验¶

1. 实验设置¶

Architecture variants¶

我们构建了三个不同参数规模的 Zipformer 模型：small (Zipformer-S)， medium (Zipformer-M)，large (Zipformer-L)。对于 Zipformer 的 6 个 stack，注意力头的数量为 {4,4,4,8,4,4}，卷积核大小为 {31,31,15,15,15,31}。对于每个注意力头，query/key 维度为 32，value 维度为 12。我们通过调节 encoder embedding dim，层的数量，feed-forward hidden dim 来得到不同参数规模的模型：

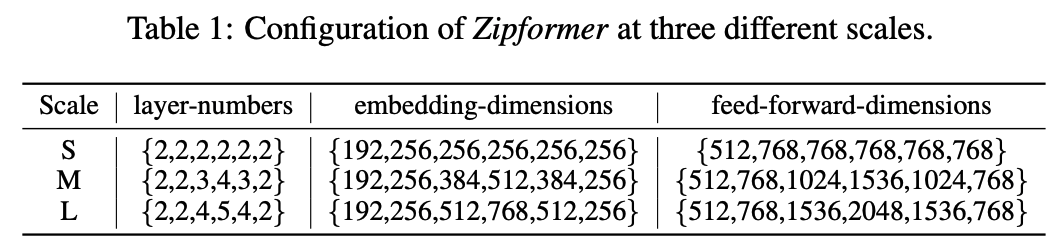
表 1：不同规模 Zipformer 的参数配置

数据集¶

我们在三个常用的数据集上进行实验：1）Librispeech，1000 小时英文数据；2）Aishell-1，170 小时中文；3）WenetSpeech，10000+ 小时中文数据。

实现细节¶

我们通过 Speed perturb 对数据进行三倍增广，使用 Pruned transducer 作为 loss 训练模型，解码方法为 modified-beam-search（每帧最多吐一个字，beam size=4）。

默认情况下，我们所有的 Zipformer 模型是在 32GB NVIDIA Tesla V100 GPU 上训练。对于 LibriSpeech 数据集，Zipformer-M 和 Zipformer-L 在 4 个 GPU 上训练了 50 epoch，Zipformer-S 在 2 个 GPU 上训练了 50 个 epoch；对于 Aishell-1 数据集，所有 Zipformer 模型都在 2 个 GPU 上训练了 56 epoch；对于 WenetSpeech 数据集，所有 Zipformer 模型都在 4 个 GPU 上训练了 14 epoch。

2. 与 SOTA 模型比较¶

LibriSpeech¶

表 2 展示了 Zipformer 和其他 SOTA 模型在 LibriSpeech 数据集上的结果。对于 Conformer，我们还列出了我们复现的结果以及其他框架复现的结果。值得注意的是，这些结果和 Conformer 原文仍然存在一定的差距。Zipformer-S 取得了比所有的 Squeezeformer 模型更低的 WER，而参数量和 FLOPs 都更少。Zipformer-L的性能显著超过 Squeezeformer-L，Branchformer 和我们复现的 Conformer，而 FLOPs 却节省了 50% 以上。值得注意的是，当我们在 8 个 80G NVIDIA Tesla A100 GPU 上训练 170 epoch，Zipformer-L 取得了 2.00%/4.38% 的 WER，这是我们了解到的迄今为止第一个和 Conformer 原文结果相当的模型。

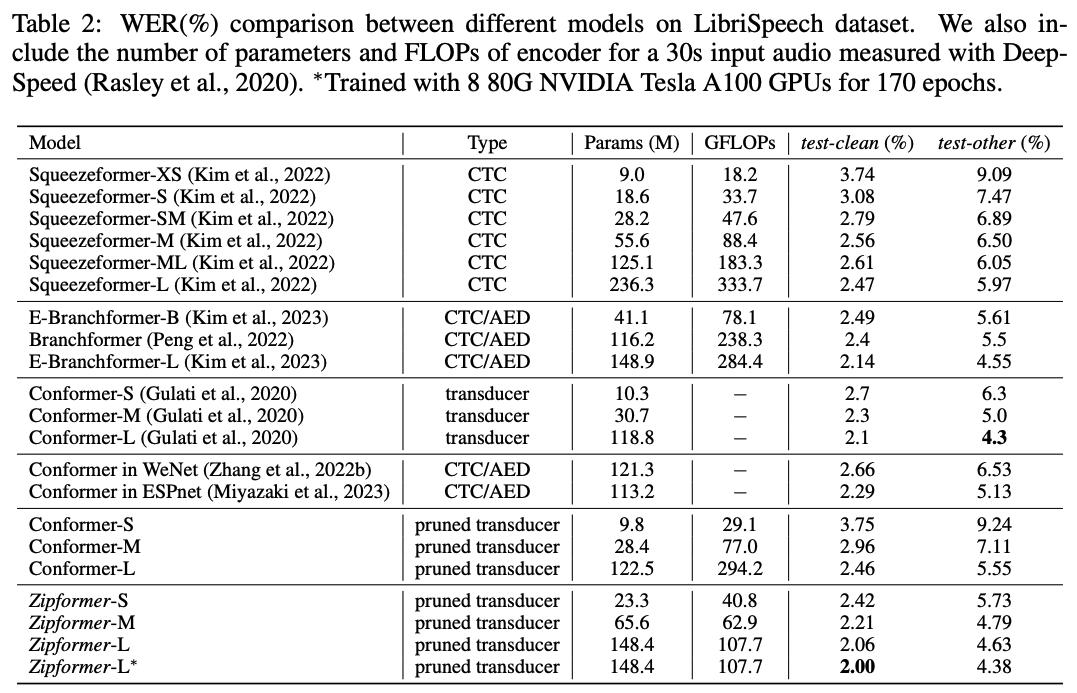
表2：不同模型在 LibriSpeech 数据集的比较

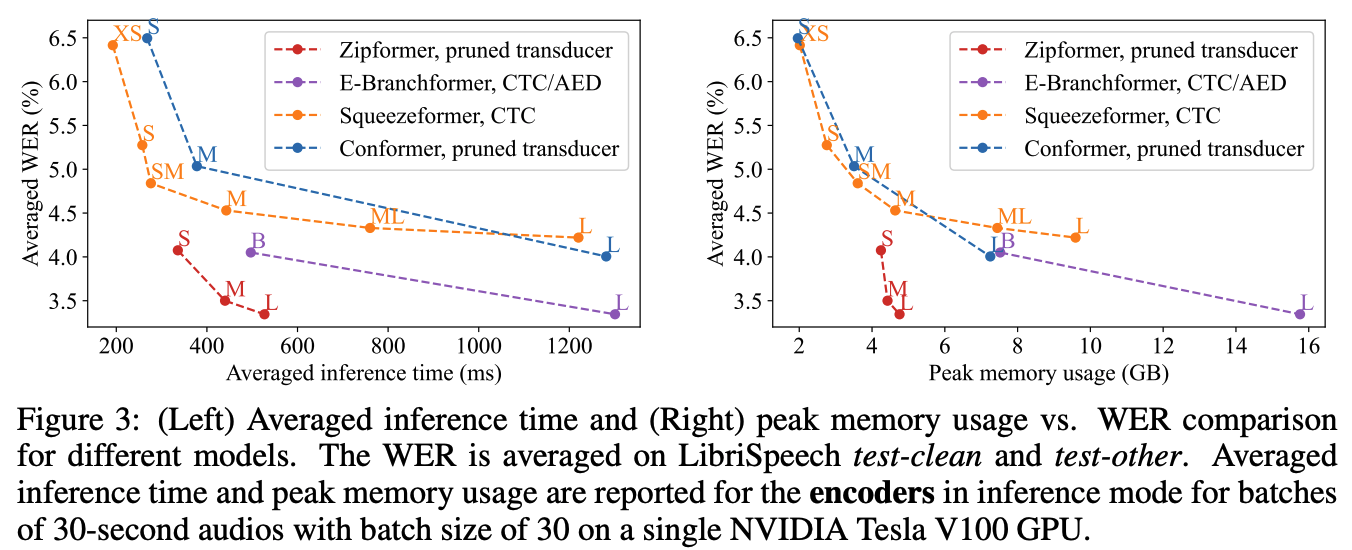
我们还比较了 Zipformer 和其他 SOTA 模型的计算效率和内存使用。图 5 展示了不同 encoder 在单个 NVIDIA Tesla V100 GPU 上推理 30 秒长的语音 batch 所需的平均计算时间和峰值内存使用量，batch size 设置为 30，确保所有的模型都不会 OOM。总的来说，与其他的 SOTA 模型比较，Zipformer 在性能和效率上取得了明显更好的 trade-off。尤其是 Zipformer-L，计算速度和内存使用显著优于其他类似参数规模的模型。

此外，我们在论文附录中也展示了 Zipformer 在 CTC 和 CTC/AED 系统中的性能，同样超过了 SOTA 模型。 CTC/AED 的代码在 https://github.com/k2-fsa/icefall/pull/1389。

图 5：不同模型的计算速度和内存使用比较

Aishell-1¶

表 3 展示了不同模型在 Aishell-1 数据集的结果。相比较于 ESPnet 框架实现的 Conformer，Zipformer-S 性能更好，参数更少。增大参数规模后，Zipformer-M 和 Zipformer-L 都超过了其他所有的模型。

表 3：不同模型在 Aishell-1 数据集的比较

WenetSpeech¶

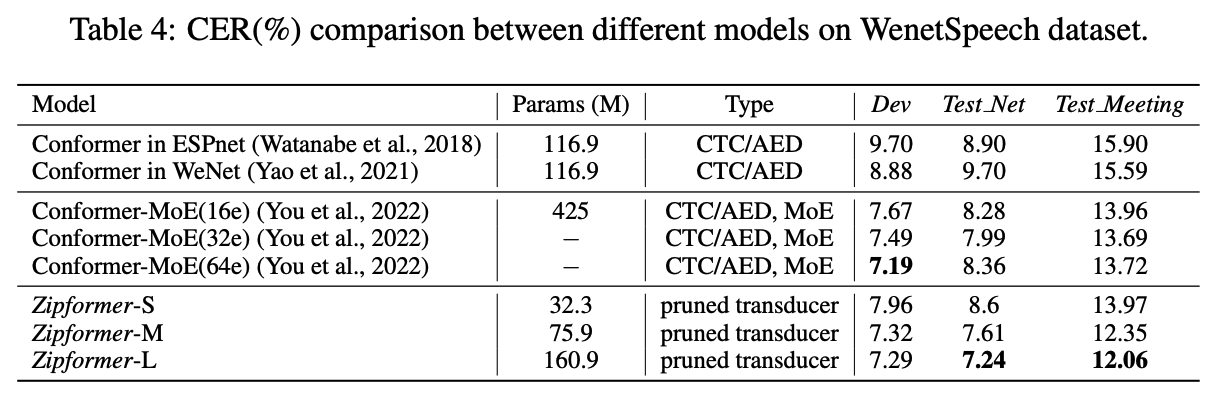
表 4 展示了不同模型在 WenetSpeech 数据集的结果。Zipformer-M 和 Zipformer-L 都在 Test-Net 和 Test-Meeting 测试集上超过了其他所有的模型。Zipformer-S 的效果超过了 ESPnet 和 Wenet 实现的 Conformer，参数量却只有它们的 ⅓。

表 4：不同模型在 WenetSpeech 数据集的比较

3. 消融实验¶

我们在 LibriSpeech 数据集上进行了一系列消融实验，验证每一个模块的有效性，实验结果如表 5 所示。

表 5：Zipformer 消融实验

Encoder structure¶

我们移除了 Zipformer 的 Downsampled encoder structure，类似于 Conformer 在 Conv-Embed 中使用 4 倍降采样，得到一个 12 层的模型，每层的 embedding dim 为 512。该模型在两个测试集上的 WER 都有所上升，这表明 Zipformer 中采用的 Downsampled encoder structure 并不会带来信息损失，反而以更少的参数达到更好的性能。

Block structure¶

由于每个 Zipfomer block 含有两倍于 Conformer block 的模块数量，我们将每个 Zipformer block 替换为两个 Conformer block，这导致了在 test-other 上的 WER 上升了 0.16%，并且带来更多的参数量，这体现了 Zipformer block 的结构优势。移除 NLA 或者 Bypass 模块都导致了性能下降。对于移除了 NLA 的模型，当我们移除注意力共享机制，这并没有带来性能提升，反而会带来更多的参数和计算量。我们认为在 Zipformer block 中两个注意力模块学习到的注意力权重具有高度一致性，共享注意力权重并不会有损模型性能。

Normalization layer¶

将 BiasNorm 替换为 LayerNorm 导致在 test-clean 和 test-other 两个测试集上 WER 分别上升了 0.08% 和 0.18%，这表明了 BiasNorm 相对于 LayerNorm 的优势，可以对输入向量保留一定程度的长度信息。

Activation function¶

当给 Zipformer 所有的模块都是用 SwooshR 激活函数的时候，test-clean 和 test-other 两个测试集上 WER 分别上升了 0.11% 和 0.42%，这表明给那些学习 “normally-off” 行为的模块使用 SwooshL 激活函数的优势。给所有的模块使用 Swish 激活函数导致了更严重的性能损失，这体现了 SwooshR 相对于 Swish 的优势。

Optimizer¶

当我们使用 Adam 来训练 ScaledAdam 的时候，我们必须给每个模块配一个 BiasNorm 来防止模型不收敛，因为 Adam 无法像 ScaledAdam 一样很好地学习参数 scale 来放缩激活值的大小。我们给两个优化器都尝试了不同的学习率 $\alpha_{\mathrm{base}}$：ScaledAdam（0.025, 0.035, 0.045, 0.055），Adam（2.5, 5.0, 7.5, 10.0）。我们给 Adam 使用与 Conformer 原文一样的 LR schedule：$\alpha_t = \alpha_{\mathrm{base}} \cdot 512^{-0.5} \cdot \min(t^{-0.5}, t \cdot 10000^{-1.5})$。图 6 分别展示了使用 ScaledAdam 和 Adam 的模型在不同 epoch 时的平均 WER，以及对应的学习率，我们将它们最好的结果分别展示在表 5 中。与 Adam 训练的模型相比较，使用 ScaledAdam 训练的模型在 test-clean 和 test-other 两个测试集上的 WER 分别下降了 0.17% 和 0.72%，同时 ScaledAdam 收敛更快、效果更好。

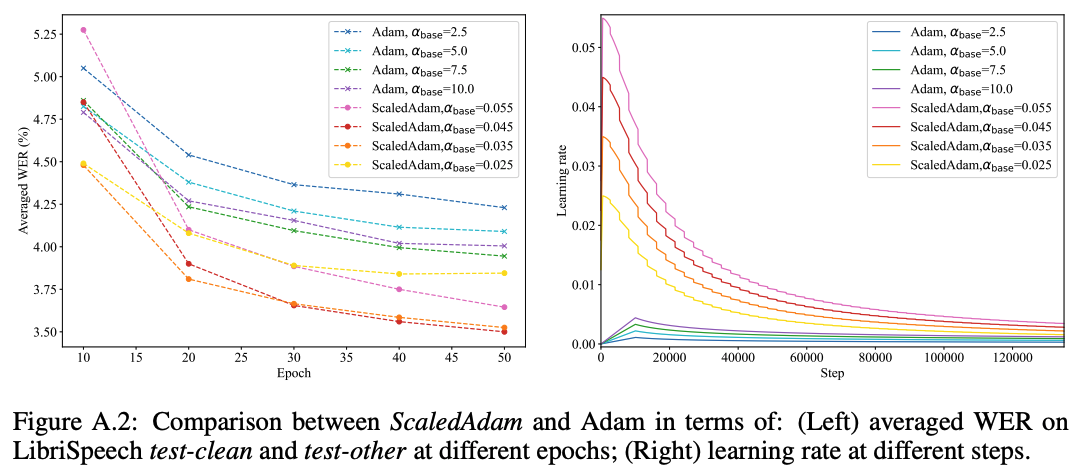
图 6：ScaledAdam 与 Adam 的比较

Activation constraints¶

如表 6 所示，我们将 Balancer 移除掉后并不会带来明显的性能变化，但是没有对激活值的范围作限制会增大模型不收敛的风险，尤其是在使用混合精度训练的时候。移除掉 Whitener 导致了在 test-clean 和 test-other 两个测试集上分别下降了 0.04% 和 0.24%，这表明通过限制激活值的协方差矩阵特征值尽可能相同，有助于让提升模型性能。

表 6

结语¶

目前，除了论文中展示的 LibriSpeech、Aishell-1 和 WenetSpeech 数据集外，我们的实验表明， Zipformer 在其它较大规模的 ASR 数据集上同样取得了新的 SOTA 结果。例如在 10000 h 的英文数据集 GigaSpeech 上，不使用外部语言模型时，在 dev/test 测试集上，66M Zipformer-M 的 WER 为 10.25/10.38，288M Zipformer 的 WER 为 10.07/10.19。值得一提的是，我们的初步实验表明，Zipformer 的相关机制（如 ScaledAdam、SwooshL 等）在语言模型和视觉模型上同样展示了有效性。

如果大家在使用 Zipformer 的过程中遇到相关问题，欢迎通过 github issue 或微信群等多个渠道反馈讨论。